缓存淘汰算法-LRU
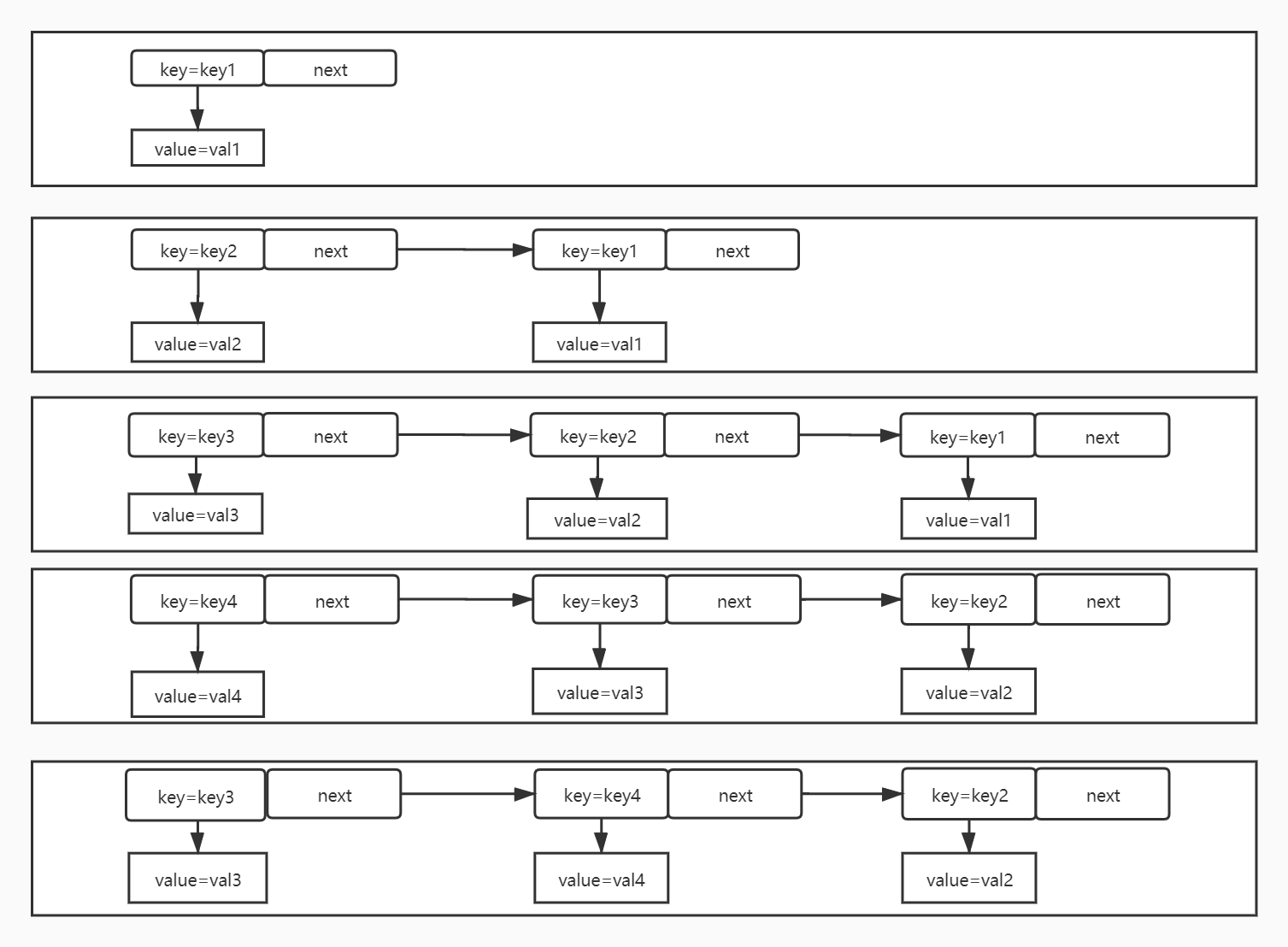
链表法
维护一个单链表,越靠近链表尾部的结点是越早之前访问的。当有一个新的数据被访问时,从链表头开始顺序遍历链表。
- 如果此数据之前已经被缓存在链表中了,我们遍历得到这个数据对应的结点,并将其从原来的位置删除,然后再插入到链表的头部。
- 如果此数据没有在缓存链表中,又可以分为两种情况:
- 如果此时缓存未满,则将此结点直接插入到链表的头部;
- 如果此时缓存已满,则链表尾结点删除,将新的数据结点插入链表的头部。
复杂度分析
无论访问的数据是否在链表中已存在,都需要遍历链表确认一遍。时间复杂度为O(n)
- 如果节点在链表中存在。将其从原来位置删除和再插入到链表头部的时间复杂度均为O(1)。
- 如果节点在链表中不存在。链表未满时,直接做链表的插入操作,时间复杂度O(1)。链表满时,先删除链表尾结点,时间复杂度O(1)。再做插入操作,时间复杂度也是O(1)。
均摊时间复杂度为O(n)
使用了除链表本身外的length和capacity来表示当前有多少个节点和一共有多少个节点,空间复杂度应为为O(1)
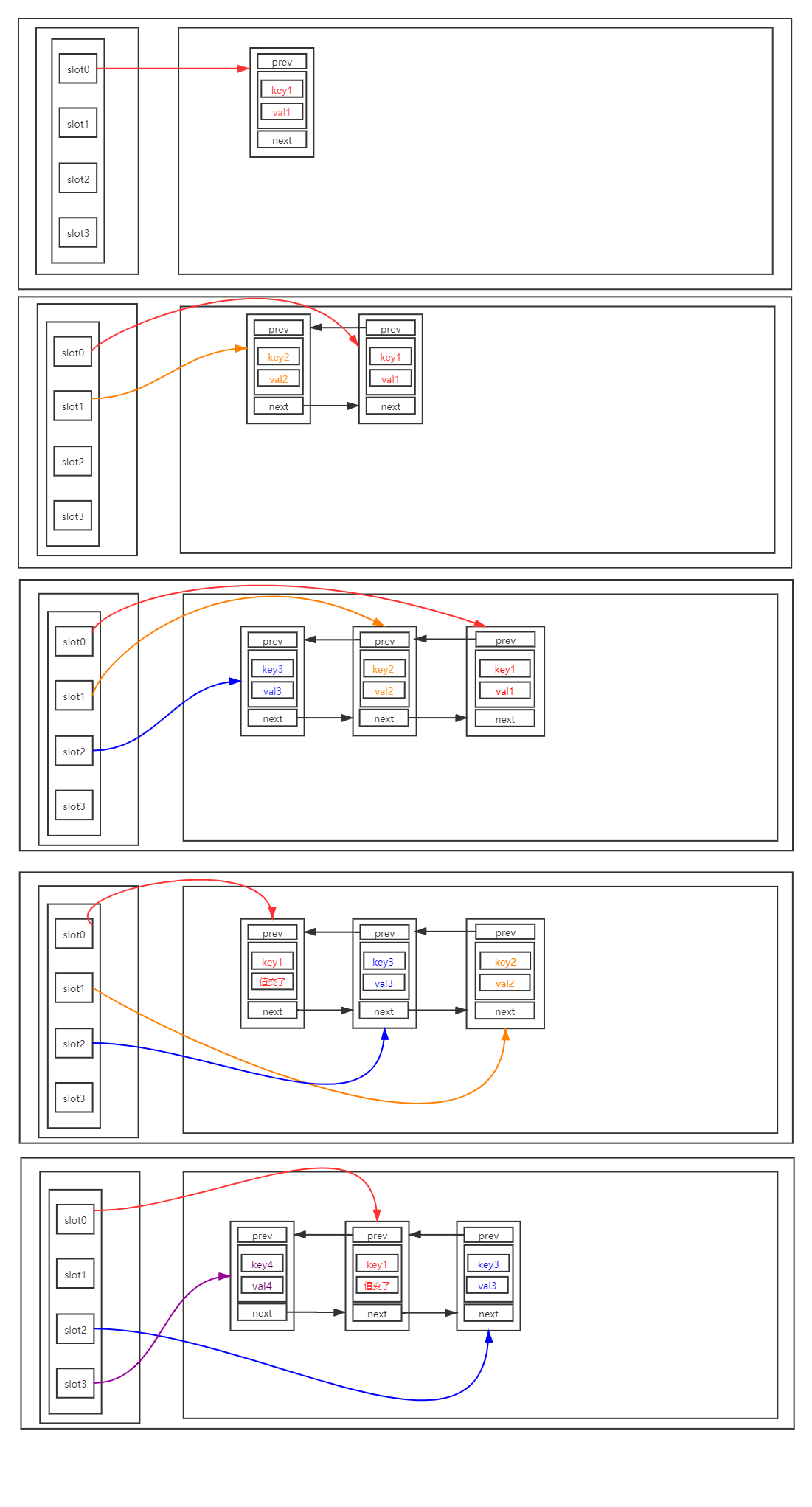
链表+散列表法
维护一个双向链表和一个哈希表。
双向链表用来维护数据,并实现LRU算法。Hash表用来降低时间复杂度。
- 如果节点在链表中不存在,则在链表中新增节点,并计算key的哈希值,将其放到hashmap中,hash表中存放该节点的指针。
- 如果节点存在,则在链表中,将其从原来的位置删除,再插入到链表头部。
- 淘汰时,删除链表尾结点,在链表头部插入新元素。
复杂度分析
查询时:
如果数据量较小的话,理论上来说,如果n个数据平均散列到m个槽上,则每个槽上的链表长度为k=n/m。时间复杂度为O(k)。
如果数据量较大的话,均匀分布下,哈希表的查询复杂度为O(1)。链表平均分布的情况下,查询时间复杂度为O(k)。均摊后,时间复杂度为O(1)。
插入和删除操作时:
因为使用了哈希表,哈希表中存放了双向链表的节点地址,所以访问链表节点的时间复杂度由O(n),降低到了O(1)。而双向链表的插入和删除操作的时间复杂度均为O(1)。所以均摊后,时间复杂度为O(1)
参考
力扣 16.25. LRU 缓存
GeekTime 数据结构与算法之美 - 20 | 散列表(下)
GeekTime 数据结构与算法之美 - 6 | 链表(上)
Demo传送门